Denosing_Diffusion_Probabilistic_Models

작성일 2023-03-11 Edited on 2023-03-13 In 생성모델

DPM (Diffusion Probabilistic Models)

이미지나 비디오 데이터에 랜덤한 노이즈를 더한 후 이를 제거하는 과정을 학습하는 모델입니다. 이를 위해 DPM은 Forward process와 Reverse process 과정을 사용합니다.
forward process (diffusion process): data에 noise를 추가하는 과정으로 Markov Chain을 통해 점진적으로 노이즈를 더해갑니다. 이 과정에서 노이즈 텀의 분포는 가우시안 분포(Gaussian Distribution)를 다르며 노이즈의 크기는 시간에 따라 점차 감소합니다.
reverse process : 가우시안 분포에서 시작하여 점진적으로 노이즈를 제거해가는 과정입니다.

딥러닝에서 데이터셋을 분석하고 모델링을 하기 위함과 새로운 데이터에 대한 예측과 생성과 같은 현실 세계에서의 복잡한 데이터셋의 확률분포(probability distribution)로 표현하는 것은 매우 중요합니다.

데이터셋의 확률분포를 구하기 위해서는 데이터셋의 특성과 분포를 파악해야 합니다. 이 과정을 통해 확률 분포를 선택하고 모델링을 할 수 있습니다. 이 때, 두 가지 요소인 tractability와 flexibility가 중요합니다.

Tractability: 모델의 계산 봅잡성에 대한 개념으로, 모델이 복잡해질수록 계산이 더 어려워집니다. 따라서 모델이 tractable하다는 것을 효율적으로 수행할 수 있으며, 실제 환경에서 사용 가능한 모델이라고 해석을 해볼 수 있습니다. 예를 들어 딥러닝 모델에서는 다양한 layer와 parameter로 구성된 복잡한 구조를 가질 수 있기 때문에, 이 모델의 tractability는 매우 중요합니다. 만약 모델이
Flexibility: 모델이 얼마나 다양한 문제를 해결할 수 있는지에 대한 개념입니다. 즉, 모델이 얼마나 유연하고 적응력이 있는지를 나타냅니다. 예를 들어, 베이지안 네트워크 모델은 여러가지 유형의 데이터에 대해 적용 가능하며, 다양한 문제에 대한 해결책을 제공할 수 있기 때문에 매우 유연하고 flexible한 모델입니다. 반면에 Linear Regression 모델ㅇ른 매우 간단한 모델이기 때문에 flexibility가 제한적일 수 있습니다.

따라서 tractability와 flexibility는 모델의 특성과 사용 용도에 따라서 모두 중요한 개념이며 이를 적절하게 고려햔 모델을 선택여 학습을 진행해야 합니다.

하지만 이 둘은 서로 trade-off 관계에 있기 때문에 실제로 모델링을 하고 학습을 진행해보면 이 둘을 동시에 만족 시키기는 어렵습니다.

그래서 초기 diffusion model인 DPM(Diffusion Probabilistic Models)는 diffusion process를 통해 가우시안 분포를 target 데이터 분포로 변환해주는 Markov Chain을 학습시켜 flexible하면서 tractable한 분포를 구하고자 했습니다.

Diffusion Model

Diffusion Model은 최근 이미지 생성을 위해 사용되는 생성모델 중 하나입니다. 이 모델은 두가지 process를 사용합니다.

forward process: data로 부터 noise를 조금씩 더해가며 data를 가우시안 분포를 따르는 noise로 만드는 과정.
reverse process: noise로 부터 data를 만들어 내는 과정.
이 두 과정을 통해 이미지 생성하는 방식을 사용합니다.

Forward Process(=Diffusion Process; $q$)

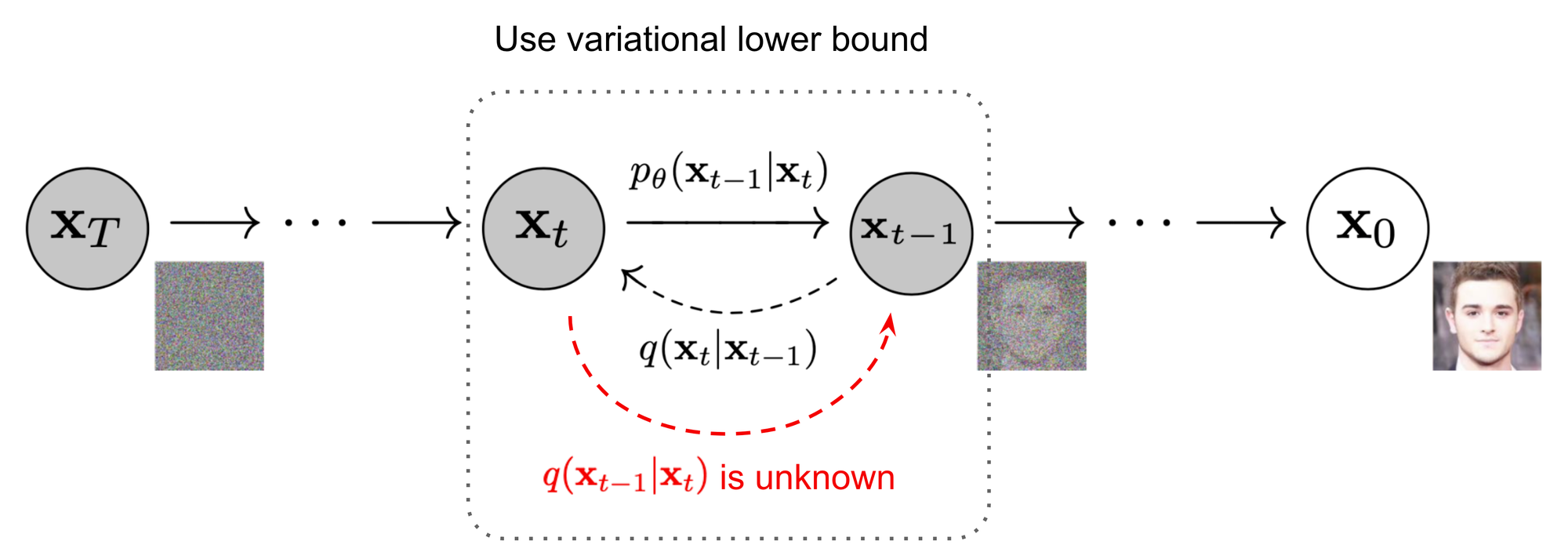- 위 과정은 `Forward Process`로 $q$라고 표시합니다. 이는 `markov chain`으로 data $x_0$에 noise를 점진적으로 추가하여 최종적으로 noise $X_T$형태로 가는 과정입니다. > Q. Sampling의 반대방향인 forward process 과정의 분포를 알아야 하는 이유는? > `reverse process의 학습을 위해 forward process 정보를 활용`하기 때문입니다.

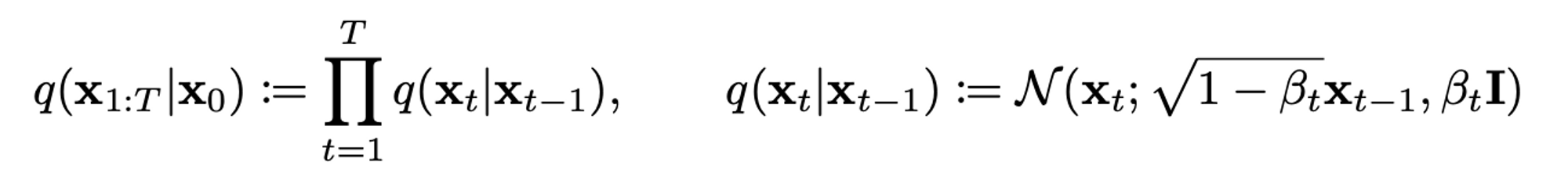
data에 noise를 추가할 때 variance schedule $\beta_1, …., \beta_T$를 이용하여 scaling한 후 data에 noise를 추가합니다.
- 이 과정은 매 step마다 가우시안 분포에서 reparameterization을 통해 sampling 하는 것을 의미하며, 이는 생성 모델에서 noise term을 추가하는 과정을 의미합니다. 이로 인해 noise를 추가하여 dissufion model이 더욱 다양한 이미지를 생성할 수 있도록 합니다. 이때 단순히 noise만 더해주는게 아니라 variance가 발산하는 것을 막기 위해 variance schedule를 이용하여 $\sqrt{1 - \beta_{t}}$로 scaling하게 됩니다.
- forward-reverse process는 DDPM(Denosing Diffusion Probabilistic Models)에서 이미지 생성 및 노이즈 샘플링 과정을 의미합니다. 이 과정에서 이미지가 생성되고 생성된 이미지와 원래 이미지간의 차이가 계산됩니다. 그 다음 이 차이에 대한 노이즈가 샘플링되어 다시 이미지에 추가합니. 이 과정에서 노이즈의 분산이 일정 수준 이상으로 커지면서 즉, 발산하게되어 이미지가 실제 이미지와 다르게 생성됩니다. 따라서 위에서도 언급한 variance schedule을 이용해서 분산이 발산하는 것을 막기 위해 variance=1로 scaling 함으로써 forward-reverse process에서 noise variance를 일정 수준 이하로 유지할 수 있게 됩니다. 이 과정으로 인해 결국 더 나은 이미지 생성이 가능해지게 됩니다.
  
  😎 매 step마다 가우시안 분포에서 reparameterization trick을 통해 sampling 하는 이유
  noise sampling 과정을 변환해서 gradient를 계산(=backpropagation 가능)할 수 있습니다. 이를 통해 model이 학습하는 동안 noise term이 고정된 값이 아니라 계속 변화하며 학습할 수 있게 됩니다. 일반적인 샘플링 방법을 사용해서 생성된 이미지는 gradient를 계산할 수 없게 됩니다. 따라서 매 step마다 가우시안 분포에서 reparameterization trick을 통해 sampling 하게 됩니다.
  
  😎 Variance schedule
  forward-reverse process에서 샘플링 과정에서 발생하는 noise의 분산이 발산하는 것을 막기 위해 즉, noise의 분산을 조절하는 방식으로 noise를 추가할때마다 분산을 감소시키며 이미지의 픽셀값을 업데이트 합니다. 이를 통해 이미지 생성 과정에서 noise를 제거하며 생성된 이미지 품질이 향상되게 됩니다.
  
  가우시안 분포를 점진적으로 더해가는 과정인 conditional gaussian distribution에서 variance=1로 맞추기 위해서 위한 수식은 다음과 같습니다.
  
  $$Var(aX) = a^2Var(X)$$
  
  위 수식을 기반으로 해보면 $(\sqrt{1-\beta_{t}})^2 +(\sqrt{\beta_{t}})^2 = 1$이 성립됩니다. 즉, 이 수식의 의도는 어던 $X_t$ 분포는 variance가 항상 1이 되도록 weight $a$,$b$를 $\sqrt{1-\beta_{t}}$, $\sqrt{\beta_{t}}$로 설정한 것 입니다.
  
  $$x_t = \sqrt{1-\beta_{t}}x_{t-1} +\sqrt{\beta_{t}} * \epsilon$$
- 위 수식은 가우시안 분포에서 reparameterization trick을 통해 샘플링하는 방법입니다.
  확률분포로부터 샘플을 생성하는데 사용됩니다. $x_t$는 $t$번째 step에서 생성된 샘플을 나타내며 $x_{t-1}$은 이전 스텝에서 생성된 샘플입니다. 또한 $\epsilon$는 평균=0 분산=1인 가우시아 분포에서 부작위로 추출한 noise값 입니다.
- reparameterization trick은 사실 VAE에서 먼저 나온 개념입니다. 딥러닝에서 사용하는 이유는 backpropagation이 가능하게 하기 위함입니다. 표준 정규분포로 어던 분포를 뽑아내서 학습하면 안 되니 backpropagation이 되도록 $\epsilon$을 더해줍니다. 즉, $x_t$는 $\mu$ + std * noise로 표현 가능합니다.
- 위 값은 학습 가능한 learnable parameter로 둘 수 있었습니다. 하지만 논문을 읽어보면 실험을 해보니 상수값으로 두어도 큰 차이가 없어 constant로 두었습니다.
- schedule 종류 중 DDPM 논문에서는 linear schedule을 사용했습니다. 이는 $\beta$를 어떻게 스케줄링 하느냐에 따라 노이즈화 하는 방식(=forward process)이 달라지게 됩니다. 즉, 논문에서는 데이터가 이미지와 비슷할 때에는 이 값을 매우 작게 설정하다가 가우시안 분포에 점점 가까워질수록 이 값을 크게 설정해 $\beta_1$ = $10^{-4}$ to $\beta_T$ = $0.02$로 설정해 linear하게 증가하도록 했습니다. 하지만 최근 들어선 linear는 너무 빠르게 노이즈로 변경되는 느낌이 있어 천천히 변경되기 위해 cosine schedule를 사용한다고 합니다.

Reverse Process($p$)

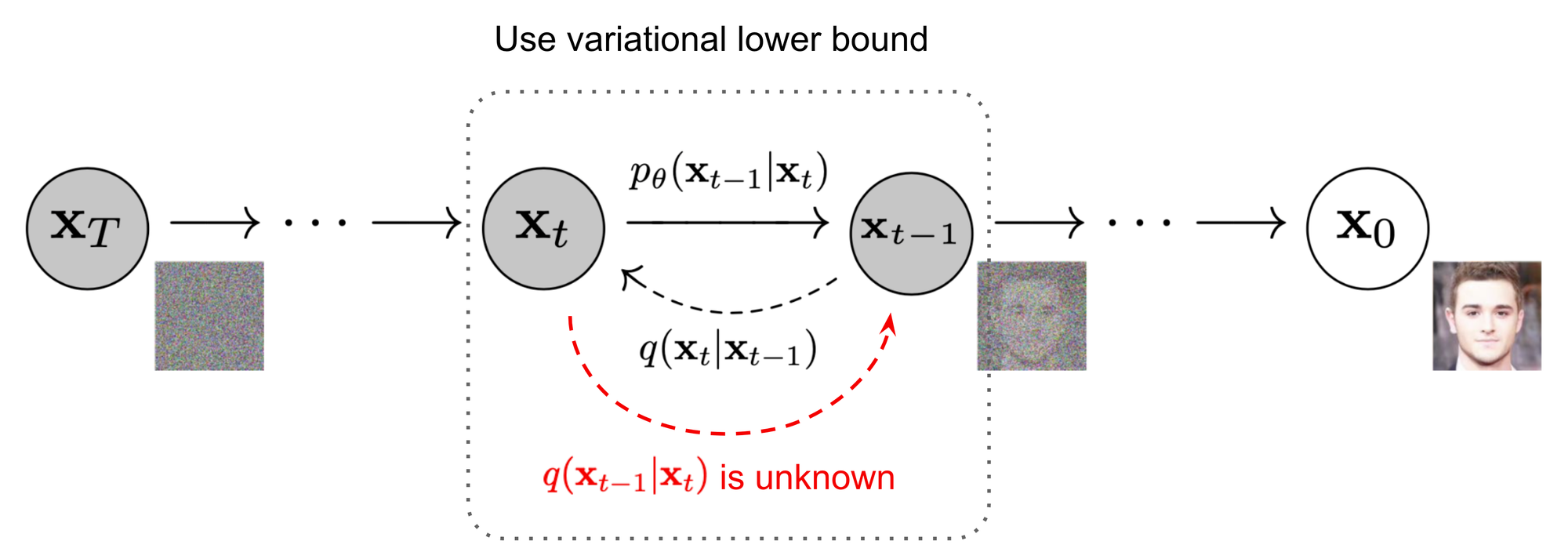
reverse process는 $p$라고 표시합니다. 위 그림에서는 $p_{\theta}(x_{t-1}|x_t)$를 의미합니다. 이는 $p_{\theta}(x_{t-1}|x_t)$를 학습함으로써 noise $x_T$로 부터 노이즈를 제거해 $x_0$를 복원하는 과정을 학습합니다.
최종적으로 random noise로 부터 data를 생성하는 생성 모델로 사용되기 때문입니다. diffusion model을 사용하기 위해서는 modeling 하는 것이 필수적이지만, 이를 실제로 알아내는 것은 쉽지 않습니다. 그래서 reverse process의 학습을 위해 forward process 정보를 사용합니다.
forward process를 설명할 때 다음과 같은 내용은 언급했습니다.

Q. Sampling의 반대방향인 forward process 과정의 분포를 알아야 하는 이유는?
reverse process의 학습을 위해 forward process 정보를 활용하기 때문입니다.

즉, $q(x_{t-1} | x_t)$를 알고 싶지만 이를 알기는 어려우니 forward proceses의 정보를 활용해서 이와 유사한 $p_{\theta}(x_{t-1}|x_t)$의 parameter를 예측 및 학습할 수 있습니다.
이 말은 주어진 noise에 대해 어떻게 점진적으로 제거할지에 대한 방법을 찾아 실제 데이터의 분포인$p_{\theta}(x_0)$를 찾는게 목적입니다. 따라서 이를 해결하기 위해 reverse process의 학습을 위해 $p_{\theta}$을 이용합니다.

이를 좀 더 자세하게 알아보도록 하겠습니다.
$p_{\theta} (x_{t-1} | x_t)$는 $x_t$가 들어왔을 때 $x_{t-1}$을 예측할 수 있게 된다면 $x_0$를 예측할 수 있습니다. 이 과정은 평균과 분산의 parameter를 갖는 가우시안 분포에 대해 이루어집니다.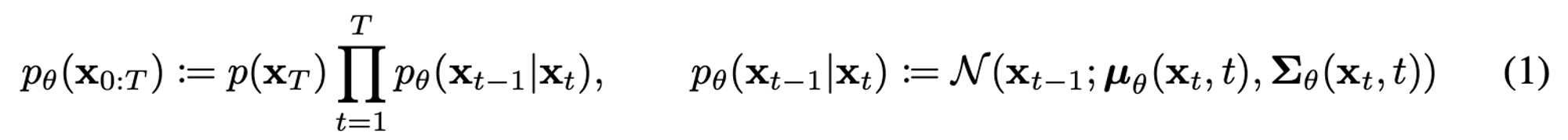
위 수식에서 각 단계의 `정규분포의 평균과 표준편차는 학습되는 learnable한 parameter`입니다.

Diffusion models and denoising autoencoders

Object Function

forward-reverse process DDPM에서 이미지 생성 및 노이즈 샘플링을 하기 위해서는 diffusion model을 학습해서 $p_{\theta}$의 parameter를 추정해야 합니다.
실제 데이터 분포인 $p_{\theta}(x_0)$을 찾아내는 것이 목적입니다. 이를 위해서 생성된 이미지의 log likelihood를 최대화 하는 방법으로 여기서는 negative log likelihood를 최소화 하는 방법을 취하고 있고 그에 대한 수식은 다음과 같습니다.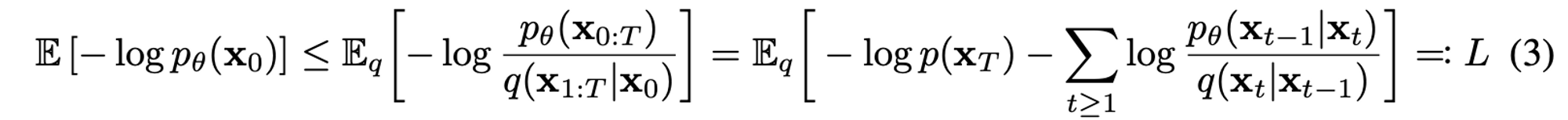
또한 training loss의 세 번째 등호는 우리가 reverse process와 forward process를 Markov chain으로 정의했기 때문에 Markov property에 의해 성립합니다.

😎 Markov property
Markov property는 많은 확률 모델에서 중요한 개념 중 하나입니다. 대표적으로 Markov chain는 markov property를 따르는 확률 과정으로 이전 상태에 의존하지 않고 현재 상태에만 의존하여 다음 상태를 결정하게 됩니다. 또한 Markov property는 불필요한 정보를 배제하여 모델의 복잡도를 줄일 수 있습니다.
DDPM은 생성한 분포와 실제 분포간의 차이를 최소화 하는게 목표입니다. 이를 위해 negative log likelihood를 최소화 하는 방법으로 loss function을 취하지만 이를 좀 더 쉽게 하기 위해 가우시안 분포 간의 KL divergence를 사용하게 됩니다. 이를 통해 학습 과정에서 noise term의 분포를 더 잘 학습할 수 있게 됩니다. 이를 통해 더 정확한 이미지 생성이 가능하게 됩니다.
그래서 최종적으로 사용하는 Loss Function은 다음과 같습니다.

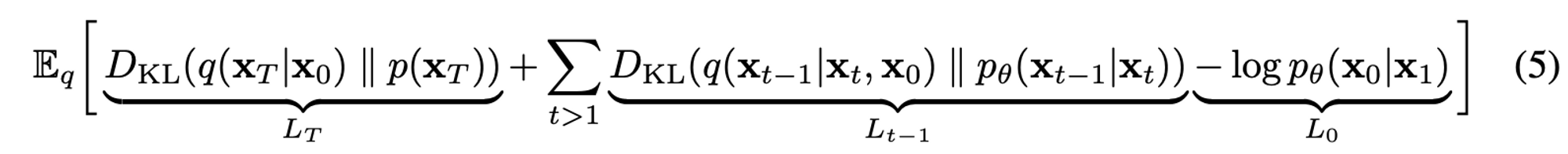
위 수식을 살펴보면
- $L_T$: Regularization term
- $L_{t-1}$: Denoising Process
- $L_0$: Reconstruction term
  
  ⭐️ Denosing Process를 보면 $x_0$로 부터 시작해 conditional하게 식을 전게하면 forward process posterior $q(x_{t-1} |x_t, x_0)$의 정규분포를 알 수 있습니다. 이를 바탕으로 KL divergence를 계산하면 우리가 결과적으로 학습 하고자 하는 $p_{\theta}(x_{t-1}|x_t)$를 학습시킬 수 있습니다.
  
  forward process posterior
  Forward process는 원래 이미지에서 시작하여 노이즈를 추가하여 이미지를 점진적으로 생성하는 과정입니다. 이 과정에서 forward process posterior는 현재 이미지와 노이즈 term의 결합 확률 분포입니다. 이를 통해, 노이즈 term의 평균과 분산을 추정하여 다음 이미지를 생성하기 위한 노이즈 term을 샘플링합니다. Forward process posterior는 다음 이미지를 생성하기 위해 필요한 중요한 역할을 합니다.

Object Function($L_T$)

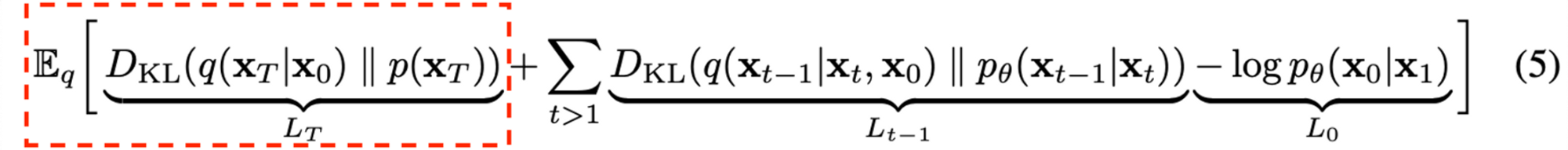논문을 읽어보면 forward process variances $\beta$를 learnable한 parameter로 두는것이 아니라 상수로 두기 때문에 $L_T$ 고려 안해도 됩니다. - 이유 - DDPM에서의 forward process는 $x_T$가 항상 가우시안 분포를 따르도록 하기 때문에 사실상 tractable한 distribution $q(x_T|x_0)$는 prior $p(x_T)$와 거의 유사합니다. 또한 DDPM에서는 forward process variance를 constant로 고정시킨 후 approximate posterior를 정의하기 때문에 이 posterior에는 learnable parameter가 없습니다. - 따라서 loss term은 항상 0에 가까운 상수이며 학습과정에서 무시됩니다.

Reverse Diffusion Process ($L_{1:T-1}$)

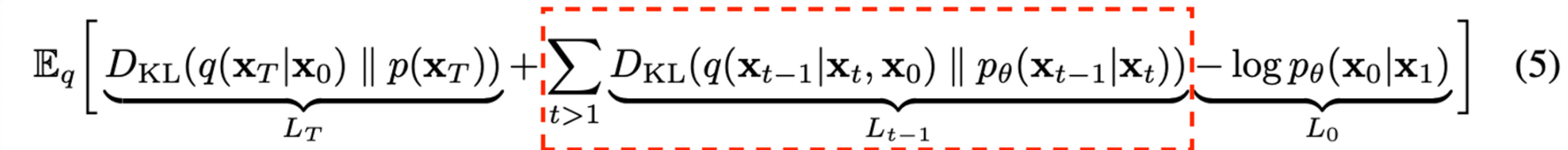위 수식을 계산하기 위해서는

$q(x_{t-1}|x_t, x_0)$의 분포를 알아내고
$p_{\theta}(x_{t-1}|x_t)$을 알아내기 위해 mean($\mu_{\theta}$), variance($\Sigma_{\theta}$)를 알아내야 합니다.
$q(x_{t-1}|x_t, x_0)$
DPM에서 알아본 내용처럼 다음과 같은 형태로 정의가 가능합니다.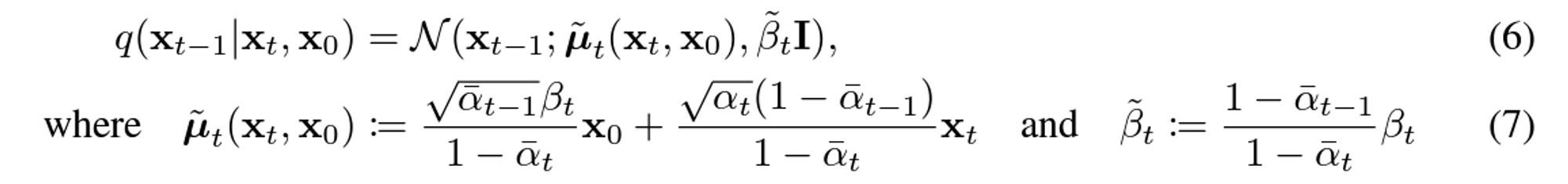
$p_{\theta}(x_{t-1}|x_t)$
- 이는 다음과 같은 형태로 정의가 가능합니다.
- $p_{\theta}(x_{t-1}|x_t) = N(x_{t-1}; \mu_{\theta}(x_t, t), \Sigma_{\theta}(x_t, t))$
$\Sigma_{\theta}(x_t, t)$
- $p$의 표준편차는 $\sigma^2_{t}I$라는 상수 행렬로 정의한다. 그러므로 이에 대해서는 학습이 필요하지 않습니다.
  
  → $\sigma^2_{t}$를 $\bar{\beta}_t$로 표현하는게 옳바르지만 $\beta$로 사용 가능
- $\Sigma_{\theta}(x_t, t) = \sigma^2_tI$
$\mu_{\theta}(x_t, t)$
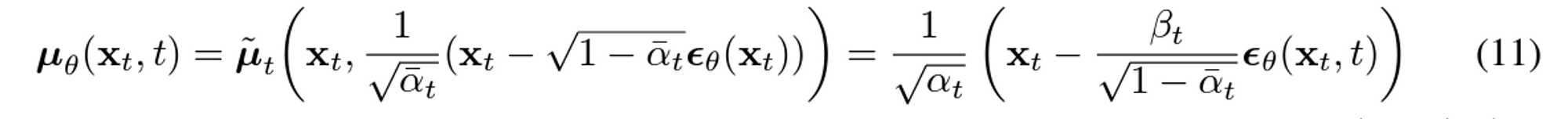
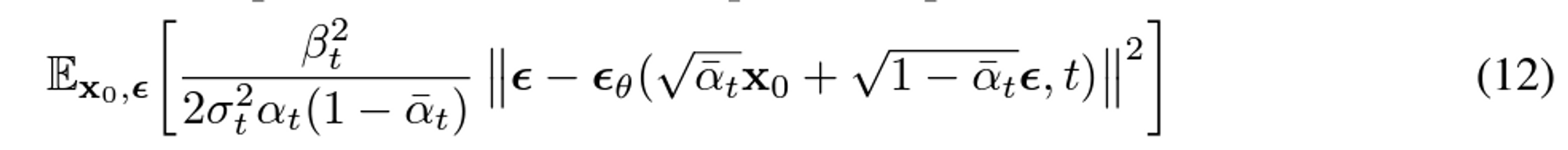
- $p$의 평균 $\mu_{\theta}(x_t, t)$는 다음과 같이 정의합니다.

요약하자면 위 Loss term에서는 $\bar{\mu_t}$를 예측하도록 reverse process mean function approximator $\mu_{\theta}$를 학습 시킵니다. 또는 $\epsilon$을 예측하도록 학습을 해도 됩니다. 논문에서 보면 저자들은 $\epsilon$을 예측하도록 loss term을 단순화하는게 성능이 더 좋다고 합니다.

😎 reverse process mean function approximator
Reverse process mean function approximator는 Variational inference를 사용하여 noise term의 사후 분포를 추정합니다. 이때, Variational inference는 Mean Function Approximator를 사용하여 noise term의 평균 값을 추정하고, 추정된 평균 값을 이용하여 noise term의 사후 분포를 근사합니다. 이를 통해 원래 이미지를 더 정확하게 추정하고, 더 나은 이미지 생성이 가능해집니다.

위 과정을 통해 $\mu_{\theta}$를 얻어내면 $p_{\theta}(x_{t-1}|x_t)$로부터 $x_{t-1}$을 샘플링 할 수 있다. 이 샘플링 알고리즘은 다음과 같이 표현이 가능합니다.

Data scaling, reverse process decoder, and $L_0$

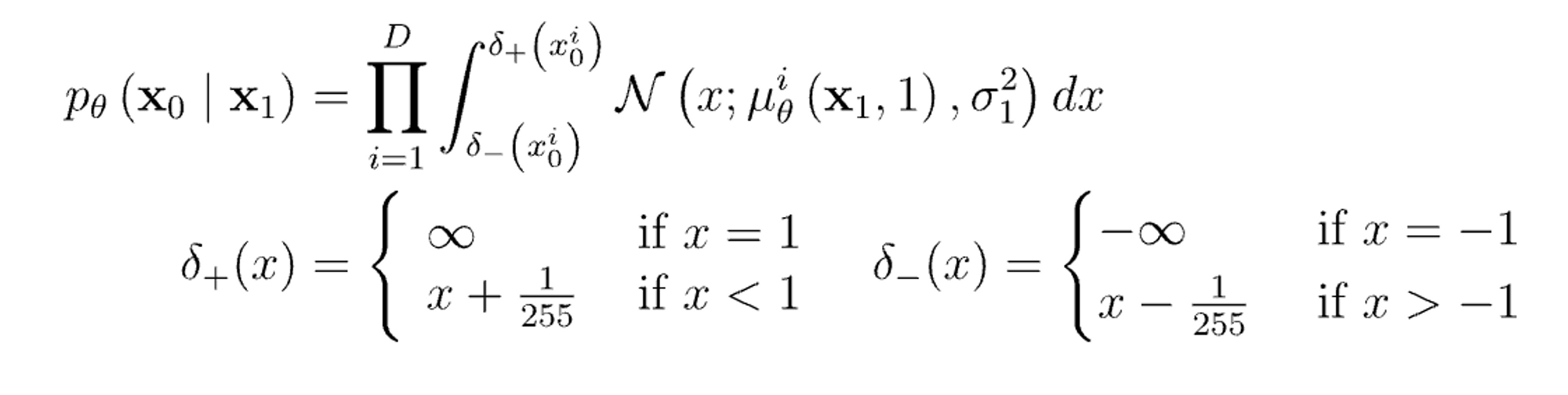
굳이 계산을 고려 하지 않을만큼 작은 값이거나 작은 상수값이라서 고려를 하지 않는건가? 라는 예측을 해볼 수 있습니다.
논문에서 학습해서 얻은 값으로 주어지기도 했지만 상수로 둔 값이랑 별 차이가 없어서 constant로 두었다고 합니다.

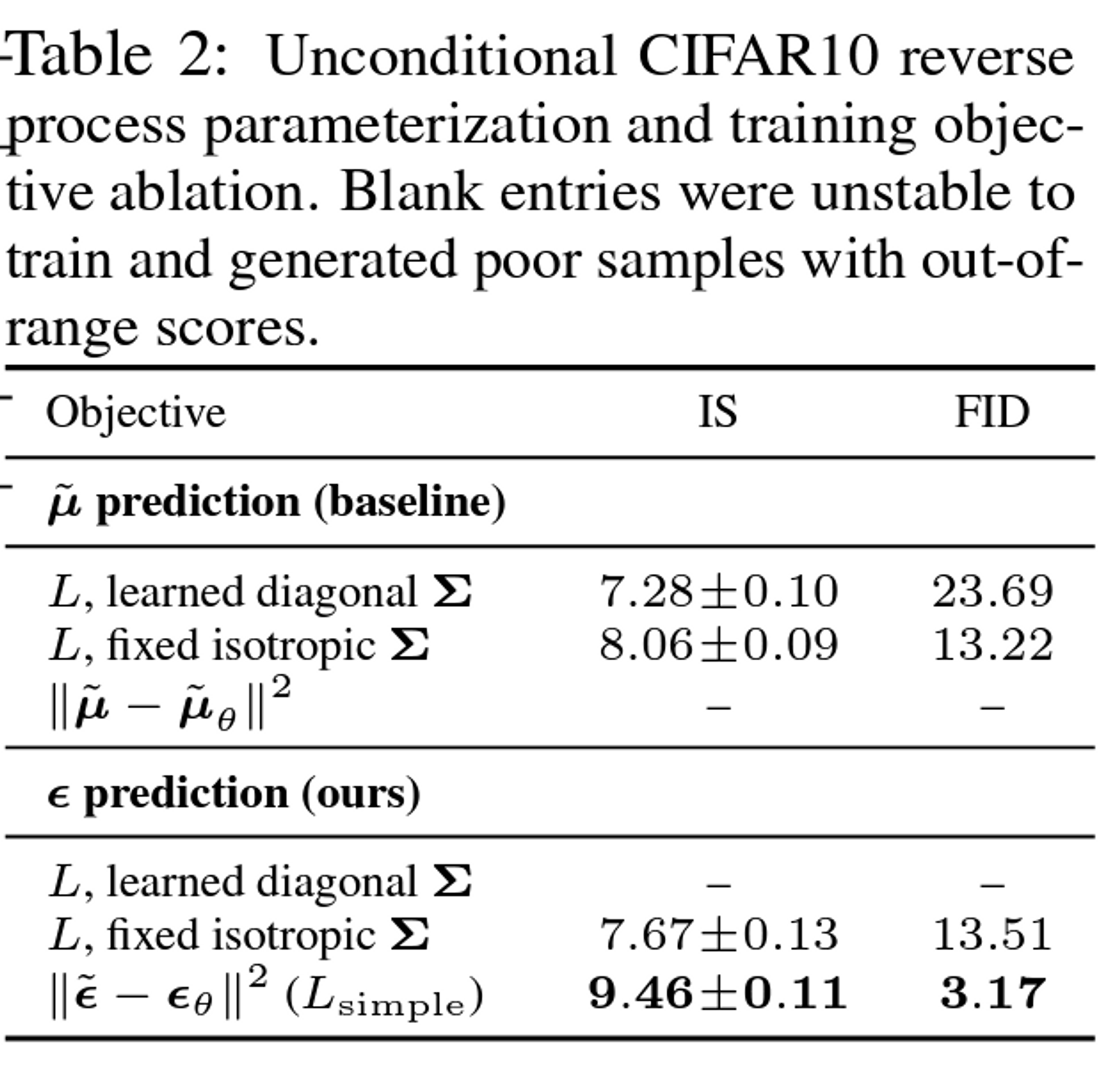
Simplified training objective

Loss function에서 중요한 term은 variational bound에 해당하는 $L_{t-1}$과 $L_0$이다. 논문에서 저자들은 해당 loss term을 아래와 같이 단순화 했다고 합니다.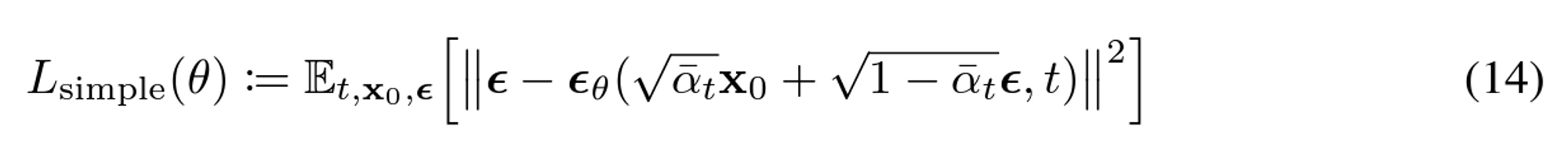

위와 같은 simplified objective을 통해 diffusion process를 학습하면 매우 작은 t 에서뿐만 아니라 큰 t에 대해서도 network 학습이 가능하기 때문에 매우 효과적입니다.

Training

noise를 더해나가는 과정으로 network $(\epsilon_{\theta}, p_{\theta})$가 $t$ step에서 noise($\epsilon$)가 얼마만큼 더해졌는지 학습합니다. 학습 시에는 특정 step의 이미지가 Gaussian noise를 얼마나 잘 denoising 되었는지 예측하도록 학습 됩니다.

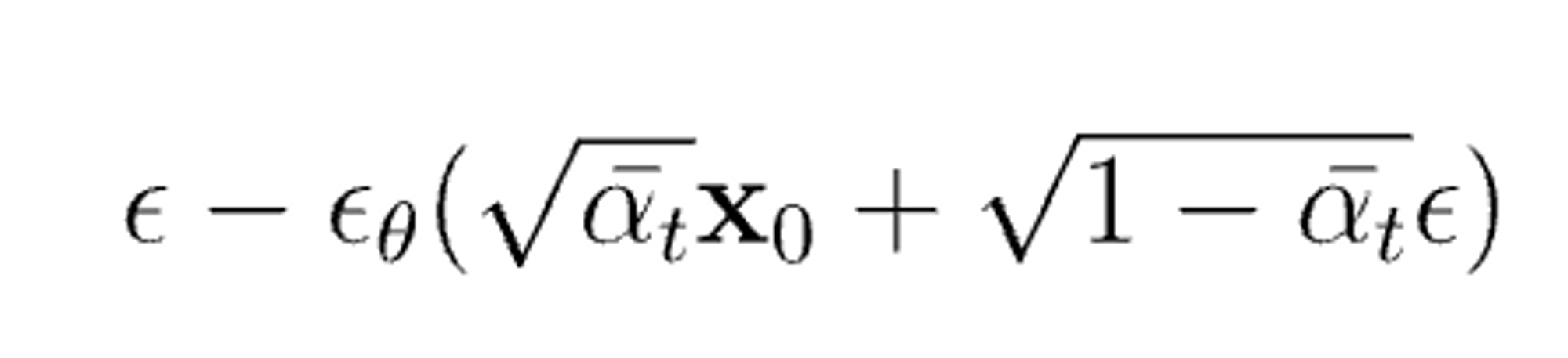$\epsilon_{\theta}$ : prediction network

정리

Forward Process($q$; image → noise)

$\mathbf{x}_t=\sqrt{1-\beta_t}\mathbf{x}_{t-1}+\sqrt{\beta_t}\epsilon, \epsilon \sim \mathcal{N}(0,\mathbf{I})$

$\beta_1=10^{-4}, \beta_T=0.02$ → 이는 linear하게 증가하고 variance schedule 이라고 부릅니다.
$\alpha_t:=1-\beta_t$,
$\bar{\alpha_t} := \prod_{s=1}^{t} \alpha_{s}$

Reverse Process($p$; noise → image)

$\mathbf{x}_{t-1}=\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta(\mathbf{x}_t, t) \Big)+\tilde{\beta}_t\epsilon, , \epsilon \sim \mathcal{N}(0,\mathbf{I})$

$\tilde{\beta_t} = \frac{1-\bar{\alpha_{t-1}}}{1-\bar{\alpha_t}}\beta_t$
$\tilde{\beta}_t=\beta_t$

Loss Function

$$\epsilon-\epsilon_{\theta}(\sqrt{\bar{\alpha_t}}\mathbf{x}_{0}+\sqrt{1-\bar{\alpha_t}}\epsilon)$$

Mulkong DeepLearning