Memory-augmented Deep Autoencoder for Unsupervised Anomaly Detection [MemAE]
- 이번 포스팅은 티스토리에서 깃블로그로 이사 후 티스토리에 정리했던 내용에서 내용을 추가해서 작성한 글 입니다. 이전 글은 Tistory에서 보실 수 있습니다.
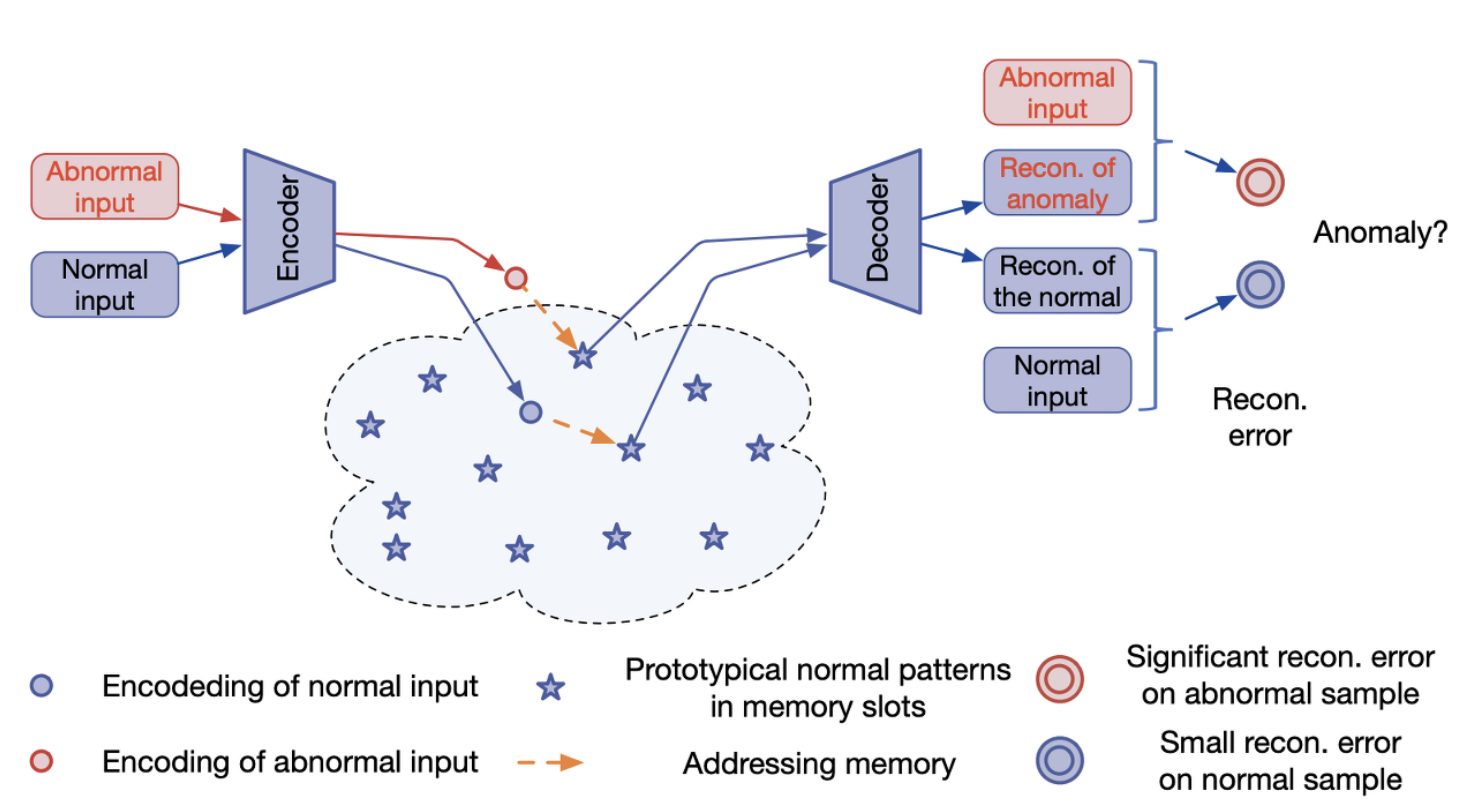
Abstract
정상 데이터를 이용하여 Autoencoder(AE)을 학습하면 정상보단 비정상 데이터에 대해 더 높은 재구성 오류(reconstruction error)을 얻게 됩니다. 하지만 AE는 일반화(Generalization)가 잘 이루어진다는 특징이 있어서 비정상 데이터가 입력되어도 정상을 재구성 해야하지만 결함이 있는 부분까지 포함하여 재구성 하는 경우가 발생하게 됩니다.
이런 AE기반 이상 탐지(Anomaly Detection)의 한계점을 개선하기 위한 해결책으로 메모리 모듈(memory module)을 사용하여 AE을 augmented 하는 방법인 MemAE을 이 논문에서는 제안하고 있습니다.
방법은 아래와 같습니다.
- 입력 $x$가 주어지면 MemAE는 먼저 Encoder을 통해 인코딩된 $z$을 얻습니다.
- 그 다음 입력된 이미지 중 메모리 모듈에서 정상 패턴인 부분에 해당하는 항목을 검색한 후
- 이를 query로 사용하여 $z$을 얻고
- 이를 Decoder을 통해 재구성 하는 방법입니다
학습 단계에서는 정상 데이터에 대한 메모리 내용(memory content)을 메모리 모듈에 기록하도록 학습이 진행됩니다.
테스트 단계에서는 학습된 메모리의 weight는 더이상 업데이트 되지 않도록 고정되고 테스트할 query가 주어지면 정상 데이터에 대한 memory record을 기반으로 재구성이 이루어집니다.
Introduction
AutoEncoder을 이용한 Anomaly Detection의 한계점
이상 탐지(anomaly detection)에서 AE는 정상 데이터의 reconstruction loss가 최소화 되도록 학습하며 테스트 과정 때 입력된 정상 데이터는 reconstruction loss가 낮고 비정상 데이터는 reconstruction loss가 커진다 라는 개념을 가정합니다.
하지만 이런 가정은 모든 상황에서 무조건 유효하지 않을 수 있습니다. 왜냐하면 AE는 general하게 학습되는 경우가 일반적이며 입력된 데이터를 그대로 복원하려는 성질을 갖고 있어서 비정상 데이터가 입력 되면 그대로 결함이 있는 상태로 재구성 하려는 성질을 갖고 있습니다.
그래서 소개하고 있는 MemAE 논문에서는 결함이 포함된 상태로 재구성 하는 문제점을 해결하기 위해 정상 데이터를 인코딩할 때 정상 데이터에 대한 메모리를 얻은 후 이를 기반으로 해서 정상 데이터를 생성하는 메모리 모듈(Memory Module)을 추가한 MemAE(Memory-augmen ted Deep Autoencoder)을 제안하고 있습니다.
Memory Module
인코딩된 vector &z&을 Decoder에 직접 전달하지 않고 아래 그림과 같이 Memory module에서 입력 데이터를 기반으로 가장 관련성이 높은 메모리 항목을 검색한 후 &z&을 query로 사용하여 Decoder에 전달 합니다.

Memory-augmented Autoencoder
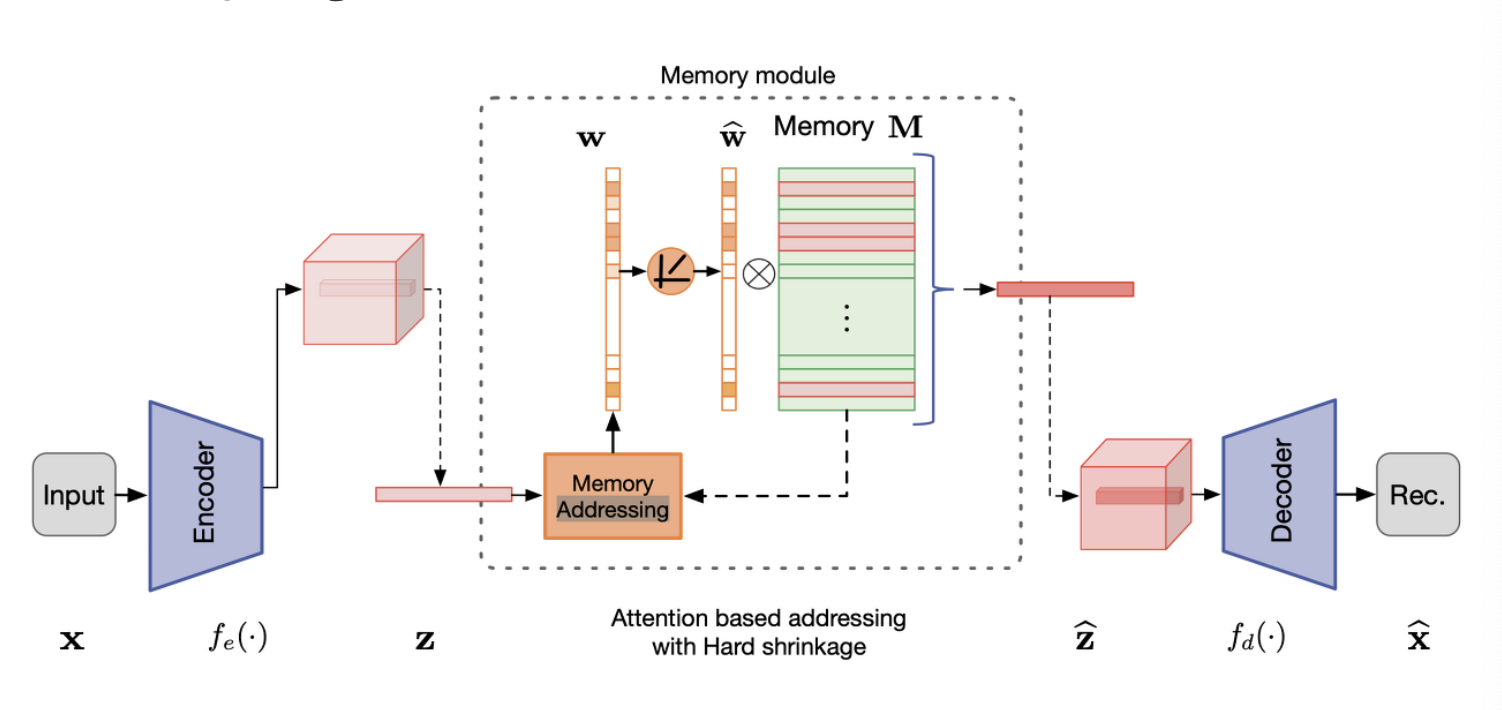
Memory module with Attention-based Sparse Addressing
이 논문에서 제안한 Memory Module의 구성 요소를 정리 해보자면 다음과 같습니다.
- soft addressing vectors $w$
- 입력된 데이터의 패턴을 Memory Address에 기록하는 vectors
- attention-based addressing operator
- 데이터의 패턴이 기록된 Memory Address에 접근하기 위한 연산자
Memory-baed Representation
입력 데이터를 기반으로 인코딩된 query $ \mathbb{Z} \in \mathbb{R}^C $가 주어지면 입력 데이터의 패턴을 Memory Address에 기록하기 위해 soft addressing vectors $ \mathbf{w} \in \mathbb{R}^{1 \times N}$을 얻습니다.
그 다음 Memory $\mathbf {M} $에 접근한 후 $\hat{\mathbf{z}}$을 얻게 됩니다. 이 과정을 식으로 표현하면 다음 수식과 같이 표현 됩니다.
$$ \hat{\mathbb{z}} = \mathbb{w}\mathbf{M} = \sum_{i=1}^N {w_i,m_i,} $$
이 논문에서는 단순 인코딩된 vector $\mathbf{z}$을 바로 디코더에 넣는게 아니라 위와 같은 과정을 거친 후 얻어진
$\mathbf{\hat{z}}$을을 디코더에 입력하여 정상 패턴만 갖고 있는 데이터를 재구성 해야 하는게 최종 목표입니다. 그러면 세부적으로 어떤 과정을 거쳐가며 위와 같은 과정이 이루어지는지 살펴보도록 하겠습니다.
Attention for Memory Addressing
메모리 모듈 $\mathbf{M}$은 학습 데이터의 정상 패턴(normal pattern)을 기록하도록 이루어져 있습니다. 정상 패턴을 기록하는 방법은 위에서 soft addressing vectors $\mathbf{w}$로 한다고 설명 드렸습니다. 이 과정을 좀 더 세분화시켜 정리를 하면 다음과 같이 정리를 할 수 있습니다.
데이터를 인코더에 입력으로 주어 인코딩된 vector $\mathbf{z}$을 얻습니다.
$\mathbf{z}$을 memory addressing 체계를 사용하여 정상 패턴을 기록합니다.
그 기록된 공간을 content addressable memory로 정의합니다.
softmax 연산을 통해 데이터 패턴을 기록하는 weight $w_i$을 계산합니다.
이 과정을 수식으로 나타내면 다은과 같이 정의됩니다.
$$ w_i = \frac{\exp{(d(\mathbf{z}, \mathbf{m_i}))}}{\sum_{j=1}^N {\exp (d(\mathbf{z}, \mathbf{m_j}))} }$$
정상 패턴을 기록하는 weight $w_i$을 얻는 수식에서 $d(.,.)$형태로 된 수식은 similarity measurement을 나타내며 이 논문에서는 cosin similarty로 정의했으며 수식은 다음과 같습니다.
$$d(\mathbf{z}, \mathbf{m_i}) = \frac{\mathbf{z} \mathbf{m_i^T}}{\parallel \mathbf{z} \parallel \parallel \mathbf{m_i} \parallel}$$
정상 패턴을 기록하는 부분은 아래 그림에 표시된 부분입니다.
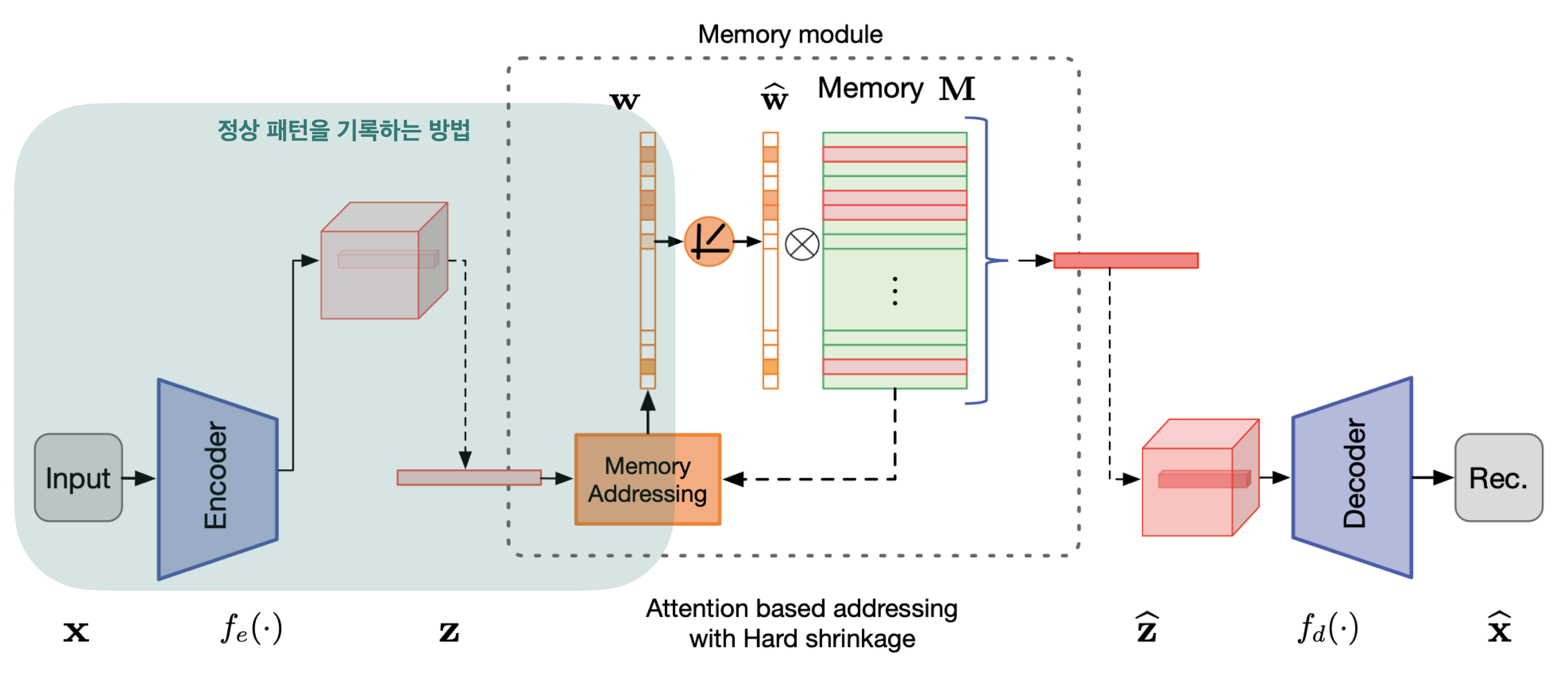
위 과정을 거치므로써 메모리 모듈 $\mathbf{M}$은 $\mathbf{z}$와 가장 유사한 메모리 항목을 검색하여 $\mathbf{\hat{z}}$을 얻게 됩니다.
적은 수의 memory items 정상 데이터를 재구성 하다
위에서 소개한 방법 중 정상 패턴을 memory addressing 체계를 사용하여 기록하는 과정은 메모리 크기가 무한대로 큰 공간에 기록하는게 아니라 제한적인 메모리 크기를 갖도록 미리 제한을 걸어둡니다.
이렇게 메모리 크기를 제한해둔 상태면 그만큼 정상 패턴에 대한 items도 많이 부족해서 정상 데이터로 재구성할 수 없게 된다는 생각이 들 수 있습니다. 하지만 이 논문에서 소개하고 있는 sparse addressing technique을 사용해서 적은 수의 정상 패턴이 기록된 addressing memory items만으로도 효과적으로 Decoder을 통해 정상 데이터를 재구성할 수 있게 됩니다.
attention-based addressing의 한계점
attention-based addressing 방법을 사용하면 정상인 부분을 효과적으로 잘 재구성 하게 됩니다. 하지만 세부적이고 미세한 결함인 부분들도 함께 재구성될 수 있게 됩니다.
그래서 이를 해결하기 위해 hard shrinkage operation을 사용하여 $\mathbf{w}$의 sparsity을 높입니다.
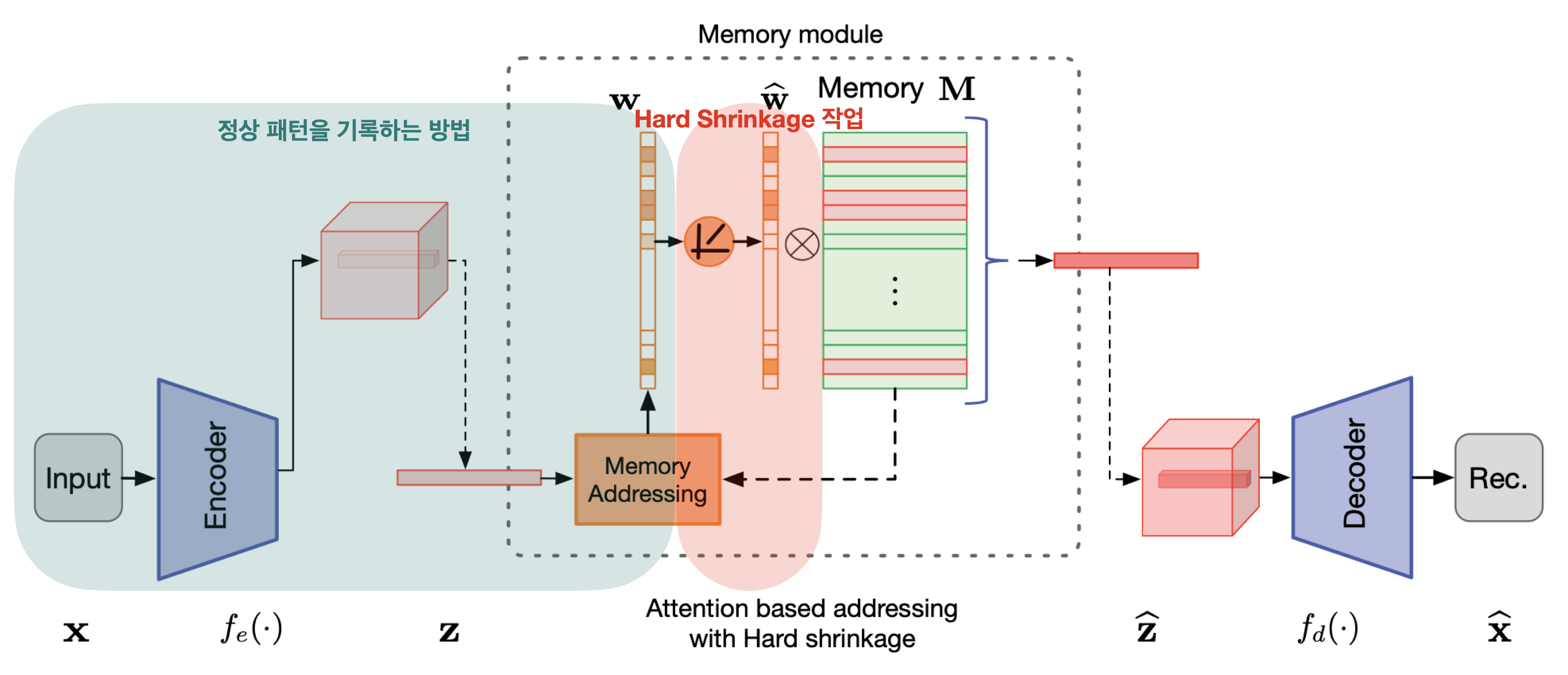
Hard Shrinkage for Sparse Addressing
Hard Shrinkage operation을 사용하는 이유는 attention-based addressing 까지만 이용한 상태의 weight $\mathbf{w}$을 이용해서 재구성을 하면 미세한 결함 부분들을 포함한 상태로 재구성이 된다는 한계점이 있었습니다.
그래서 이를 해결하고자 hard shrinkage operation을 적용하여 $\mathbf{w}$의 sparsity을 높여서 한계점을 극복할 수 있습니다.
shrinkage operation의 수식은 다음과 같습니다.
$$ \hat{w}_i = h(w_i ; \lambda) = \begin{cases} {w_i}, & \mathbf{if} \ w_i > \lambda , \ 0, & \mathbf{otherwise}, \end{cases}$$
위 수식에서 $w_i$는 attention-based addressing과정 이후 $\hat{w}$을 지정하는 메모리의 i번째 항목을 나타내며 $\lambda$는 shrinkage threshold value을 나타내는 Hyper parameter입니다.
실제로 코드를 구현할 때 threshold $\lambda$는 1/N ~ 3/N 간격으로 설정하면 최적의 결과를 얻을 수 있다고 논문에 나와있습니다.
또한 식에서 discontinuous function의 backward을 구하는 것은 쉽지 않으므로 이 논문에서는 단순화를 위해 $w$의 모든 항목이 음수가 아니라는 점을 고려해서 continuous ReLU activation function을 사용하여 Hard shrinkage을 재정의 하게 되었습니다. 그 수식은 다음과 같습니다.
$$ \hat{w}_i = \frac{max(w_i - \lambda, 0) \cdot w_i} {|w_i - \lambda | + \epsilon} $$
위 수식에서 $ max( . , 0) $는 ReLU activation function 이므로 그 값은 매우 작은 scalar 입니다.
shrinkage후 $\hat{\mathbf{w}}$을 $\hat{w_i} = \hat{w_i} / \parallel \hat{\mathbf{w}}\parallel_1 $로 re-normalize 합니다. 그러면 latent representation $\hat{\mathbf{z}} = \hat{\mathbf{w}}\mathbf{M}$을 얻게 됩니다.
학습 방법
Reconstruction loss
$$ R(\mathbf{x}^t, \mathbf{\hat{x}}^t) = \parallel \mathbf{x}^t - \mathbf{\hat{x}}^t \parallel _{2} ^2 , $$
Entropy loss
shrinkage operation 외에 학습 중 $\mathbf{\hat{w}}$에 대한 sparsity regulartizer을 최소화 합니다.
$$ E(\mathbf{\hat{w}}^t) = \sum_{i=1}^T {-w_i \cdot log(\hat{w}_i).}$$
Total loss
$$ L(\theta_e, \theta_d, \mathbf{M}) = \frac{1}{T} \sum_{t=1}^T (R(\mathbf{x}^t, \mathbf{\hat{x}}^t) + \alpha E(\mathbf{\hat{w}}^t)), $$
논문에서 실험해본 결과 $\alpha = 0.0002$가 가장 좋은 결과를 얻는다고 합니다. 또한 학습중 Memory module $\mathbf{M}$은 backpropagation & Gradient Descent을 통한 최적화가 진행 되었습니다.